こちらの記事はYoutube【ZAi探の解説動画チャンネル】でも公開中!!
よかったらチャンネル登録お願いします。
指数平滑移動平均線とは
指数平滑移動平均線(読み方:しすうへいかついどうへいきんせん)
指数平滑移動平均線とは、単純移動平均線よりも直近の価格に比重を置いた移動平均線のことです。
英語表記は「Exponential Moving Average」となり、頭文字をとって「EMA」と表記されることもあります。
単純移動平均線は、一定期間の全ての価格を平等に扱って平均値を求めるので、過去の価格と直近の価格の比重は同じになります。
一方で指数平滑移動平均線は、前日の指数平滑移動平均線と当日の終値を使って値を求めるので、過去の価格の比重は軽く、直近の価格の比重は高くなります。
直近の価格に比重を置くことで単純移動平均線よりも相場に早く反応し、トレンド転換を早めに察知することができるというメリットがあります。
但し、相場に早く反応する分、「ダマシ」も多くなるというデメリットもあります。
なお、指数平滑移動平均線は「MACD」などに応用される移動平均線としても有名です。
指数平滑移動平均線メモ
・英語では「Exponential Moving Average」といい、略して「EMA」と呼ぶこともある
・指数平滑移動平均線は相場により早く反応するのでトレンド転換を早めに察知できるほか、「MACD」などに応用される移動平均線としても有名である
指数平滑移動平均線の設定値と計算式
指数平滑移動平均線は、単純移動平均線と同じように「短期・中期・長期」の3本の線で形成されており、それぞれに数値を設定していきます。
よく利用される設定値は以下の通りです。
日足チャート:5日、25日、75日、100日、200日
週足チャート:9週、13週、26週、52週
月足チャート:6ヶ月、12ヶ月、24ヶ月、60ヶ月
基本的な設定値は単純移動平均線と変わりはありません。
たとえば、「短期(5)、中期(25)、長期(75)」といったように、短期がもっとも小さく、長期がもっとも大きい数値で設定を行います。
設定値は投資スタイルによって合う合わないもありますので、自身にあった数値で設定するようにしましょう。
それでは、指数平滑移動平均線の計算式について確認していきましょう。
指数平滑移動平均線の計算式
指数平滑移動平均線の値は、以下の計算式で求めることができます。
n=設定期間(指数平滑移動平均線の設定値)
但し、1日目の指数平滑移動平均線については、単純移動平均線と同じように全ての価格を平等に扱って平均値を求めることになります。
たとえば、次の株価推移で5日の指数平滑移動平均線を求める場合。
| 日付 | 終値 |
| 8/1(月) | 4,017 |
| 8/2(火) | 3,996 |
| 8/3(水) | 4,100 |
| 8/4(木) | 4,040 |
| 8/5(金) | 4,190 |
| 8/8(月) | 4,192 |
| 8/9(火) | 4,294 |
1日目は5日移動平均線(単純移動平均線)を求めていきますので「当日含めて5日分のデータ」が必要となります。
つまり、1日目は8/5(金)となりますので「8/1(月)~ 8/5(金)の終値」を基に値を求めていきます。
1日目の計算式は「n日分の終値の合計÷n」となるので、実際に計算をすると次のようになります。
8/5(金)の指数平滑移動平均線は「4068.60」というのがわかります。
次に8/8(月)の指数平滑移動平均線の値を求めていきます。
2日目以降は前日の指数平滑移動平均線(EMA)と当日終値を基に計算していきます。
計算式は「前日EMA+2/(n+1)×(当日終値-前日EMA)」となるので、上記データをもとにすると次のように計算できます。
8/8(月)の指数平滑移動平均線は「4109.73」というのがわかります。
以降は同じように「前日EMA」と「当日終値」を使って計算していくので、8/9(火)は次のようになります。
8/9(火)の指数平滑移動平均線は「4171.16」というのがわかります。
取引ツールでは期間を設定すれば自動的にチャート表示してくれます。
ですから特に計算式を覚えておく必要はないですが、他の移動平均線と区別するために「何を基にしたテクニカル指標なのか」という点は覚えておいても損はないでしょう。
指数平滑移動平均線の見方
実際に指数平滑移動平均線をチャート表示し、基本的な見方について確認していきましょう。
例として、楽天証券の「iSPEED」のチャートを参考にして説明していきます。
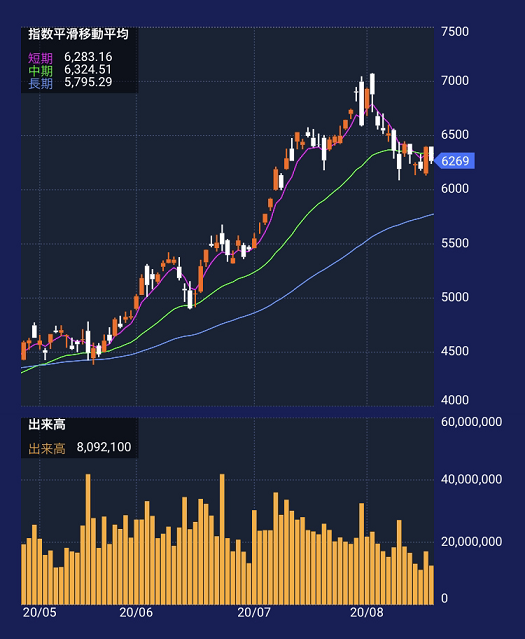
・位置関係
指数平滑移動平均線はトレンド系指標となっており、基本的には株価チャート上に表示されています。
・指数平滑移動平均線の線について
指数平滑移動平均線は「短期・中期・長期」の3本の線で形成されています。それぞれの線の向きやクロスを利用して取引に活用することができます。
・指数平滑移動平均線を見るときのポイント
指数平滑移動平均線は単純移動平均線と同じように利用しますが、単純移動平均線よりも相場に早く反応するという特徴があります。そのため、単体で利用する場合は「ダマシ」も多くなりますので、単純移動平均線と併用して分析していくのが良いでしょう。
それでは、指数平滑移動平均線の具体的な使い方について確認していきましょう。
指数平滑移動平均線の使い方
指数平滑移動平均線の使い方について説明していきます。
基本的な使い方としては単純移動平均線と同じです。
移動平均線の向きやクロスからトレンド分析し、売買の目安に利用していきます。
・指数平滑移動平均線と株価の位置関係から分析
・指数平滑移動平均線の向きから分析
・指数平滑移動平均線のクロスから分析
1つずつ説明していきます。
指数平滑移動平均線と株価の位置関係から分析
指数平滑移動平均線は、株価との位置関係からトレンド分析をすることもできます。
・株価が指数平滑移動平均線よりも上にある場合は上昇トレンド(買い)
・株価が指数平滑移動平均線よりも下にある場合は下降トレンド(売り)
上記のように考えることができます。
例としてチャートを挙げると、以下のような状態です。
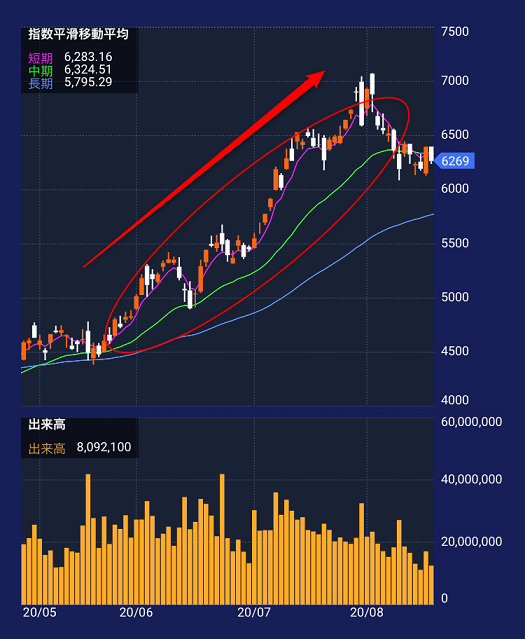
株価は25日移動平均線の上で推移しており、上昇トレンドが継続しています。
このように指数平滑移動平均線と株価の位置関係からトレンドを見ることができます。
指数平滑移動平均線の向きから分析
指数平滑移動平均線の向きから相場の強弱を分析することもできます。
・指数平滑移動平均線が上向きなら強気相場(買い)
・指数平滑移動平均線が下向きなら弱気相場(売り)
・指数平滑移動平均線が横ばいならもみ合い局面(様子見)
但し、短期・中期・長期で動きは異なります。
たとえば、以下のように5日移動平均線は下向き、25日移動平均線は上向きという状況になることもあります。
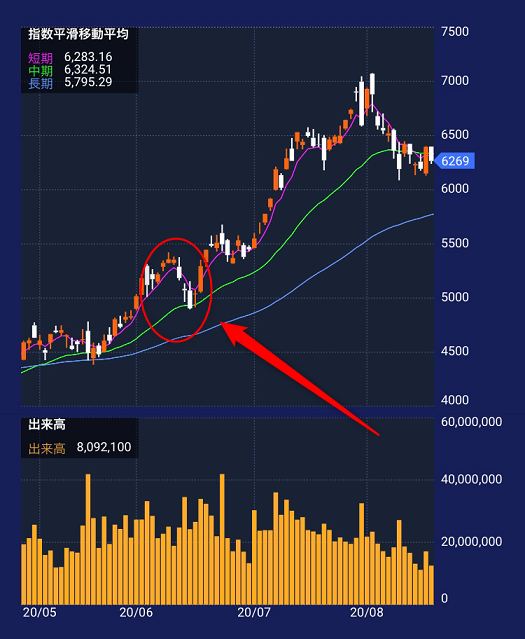
こういう場合は短期的に見ると株価の下落が見られるかもしれませんが、中長期で見ると強気相場となっているため、まだ上がるかもしれないという見方ができます。
つまり、デイトレのような短期売買をする場合は「売り」と判断することもできますが、中長期投資の場合は「買い(押し目買い)」と判断することができます。
指数平滑移動平均線のクロスから分析
指数平滑移動平均線のクロスとは、「ゴールデンクロス」と「デッドクロス」のことです。
ともに売買サインのひとつとして使われるもので、トレンドが転換した可能性が高いという見方ができます。
ゴールデンクロスは、短期の移動平均線が長期の移動平均線の下から上に抜けることをいいます。
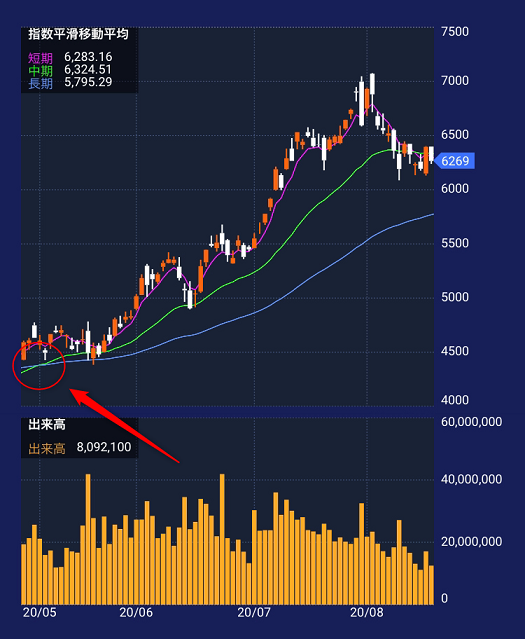
ゴールデンクロスが発生すると「下降トレンドから上昇トレンドへ転じた可能性が高い」という見方ができ、「買い」の判断をするためのひとつの目安になります。
また、上記のようにゴールデンクロス発生後、株価が指数平滑移動平均線よりも上で推移し、指数平滑移動平均線が上向きにある場合は「強い上昇トレンド」にあると考えることができます。
デッドクロスは、短期の移動平均線が長期の移動平均線の上から下に抜けることをいいます。
デッドクロスが発生すると「上昇トレンドから下降トレンドへ転じた可能性が高い」という見方ができ、「売り」の判断をするためのひとつの目安になります。
また、デッドクロス発生後、株価が指数平滑移動平均線よりも下で推移し、指数平滑移動平均線が下向きにある場合は「強い下降トレンド」にあると考えることができます。
但し、テクニカル指標は万能なものではりません。
そのため、指数平滑移動平均線を利用してテクニカル分析する場合は、他の指標と組み合わせて精度を上げたり、その他の要因も考慮して投資判断をするようにしましょう。
指数平滑移動平均線メモ
・移動平均線と株価の位置関係や移動平均線の向きからトレンドを読み取ることができる
・ゴールデンクロスやデッドクロスはトレンド転換の可能性もあり、売買サインとして捉えることができる
・但し、指数平滑移動平均線は「ダマシ」も多くなるので注意も必要である