こちらの記事はYoutube【ZAi探の解説動画チャンネル】でも公開中!!
よかったらチャンネル登録お願いします。
標準偏差とは
標準偏差(読み方:ひょうじゅんへんさ)
標準偏差とは、データのばらつき度合いを示した統計値のことです。
記号で「σ(読み方:シグマ)」と表され、テクニカル指標の「ボリンジャーバンド」でも活用されています。
英語では「standard deviation」といい、頭文字をとって「SD」と表記されることもあります。
株式等の金融市場では「投資におけるリスク」を数値化するときに使われる指標となります。
一般的にリスクとは「危険」という意味で使われますが、投資におけるリスクとは「価格の振れ幅」のことをいいます。
振れ幅が大きいとリスクが高く、小さいとリスクが低いという見方がされます。
統計学的には、株価は平均価格からある一定の範囲内で推移するとされています。
要するに株価が平均価格からぶれる可能性があるということです。
このブレ幅が投資におけるリスクとなり、「上下いくら程度ぶれる可能性があるのか」を数値化したものが標準偏差となります。
たとえば、標準偏差が「100」である場合は、平均価格から上下100円の値幅内で推移するだろうと予測されます。
冒頭で触れた「ボリンジャーバンド」は、標準偏差をチャート上に表示した指標となります。
ボリンジャーバンドでは「±1σ」「±2σ」「±3σ」といったように複数表示されていますが、これは「株価がσの範囲内に収まる確率」に違いがあります。
±1σの範囲に収まる確率は約68.3%、±2σで約95.4%、±3σで約99.7%となっています。
標準偏差メモ
・株式等の金融市場ではリスク(価格の振れ幅)を数値化するときに使われている
・わかりやすく言うと平均価格から「上下いくら程度ぶれる可能性があるのか」を数値化したもの
・テクニカル指標のボリンジャーバンドでも活用されており、記号で「σ(読み方:シグマ)」と表すこともある
標準偏差の設定値と計算式
標準偏差は「一定期間のデータ」を基に求めるので、「設定値=期間」となります。
設定期間は14や20、26などさまざまですので、投資スタイルに応じて設定するようにしましょう。
標準偏差は「分散の正の平方根」となります。
分散の求め方は、データから平均値を算出し、各データから平均値を引いて2乗し、その合計をデータの数で割って求めることができます。
噛み砕いて説明していくと、はじめにデータ(設定期間)の株価(終値)から平均価格を求めます。
設定期間5日の場合は、5日分の終値を合計して、設定期間の5で割ります。
次に設定期間のそれぞれの終値から平均価格を引いて、その値を2乗し、5日分の合計を求めて、設定期間の5で割り、分散値を求めます。
分散値を求めたら、分散の正の平方根で標準偏差を求めることができます。
たとえば、次のような株価データAがあったとしましょう。
| 日付 | 終値 |
| 9/11 | 660円 |
| 9/10 | 660円 |
| 9/9 | 652円 |
| 9/8 | 634円 |
| 9/7 | 637円 |
株価データAの標準偏差は「11.13」であることが分かります。
ボリンジャーバンドでは「±1σ」「±2σ」「±3σ」が表示されていますが、上記の計算で求めた標準偏差は「±1σ(±σ)」で使われます。
「±2σ」の数値は標準偏差に2を掛けた数値、「±3σ」の数値は標準偏差に3を掛けた数値が使われます。
標準偏差の見方
標準偏差は投資におけるリスクを見るときに使われます。
具体的には平均価格からどれくらいぶれる可能性があるのかを見るために使います。
楽天証券の「iSPEED」では、以下のように表示されています。
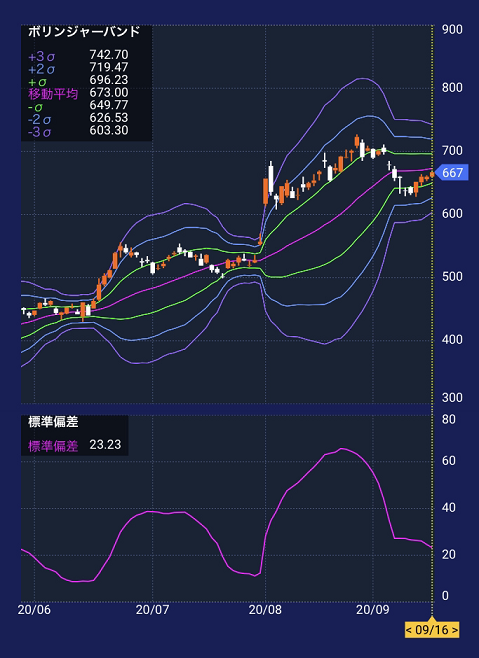
標準偏差は、基本的に株価チャートの下に表示されています。
標準偏差の数値は、「設定期間の平均値」から上下どれくらいぶれる可能性があるのかを示したものであり、現在価格や移動平均線の平均値からのブレ幅ではないので勘違いしないように注意しましょう。
一般的に株式投資で標準偏差を活用する場合は「ボリンジャーバンド」が使われます。
ボリンジャーバンドでは±1σ~±3σの帯が表示されているので、一目でぶれる可能性がある幅を把握することができます。
統計学上では「±1σ:約68.3%」「±2σ:約95.4%」「±3σ:約99.7%」の高い確率でその範囲内に収まるとされているので、株価が+σに近づいたら売り、-σに近づいたら買いといったように逆張り投資などに活用されることもあります。
ボリンジャーバンドについては「ボリンジャーバンドとは何か?わかりやすく解説」で説明しています。